Given a set of $N$ numbers, $Q = {q_1, q_2, .... q_i, .... q_N}$ such that every $q_i$ has a 50% chance of being $1$ and a 50% chance of being $-1$, find the expected value of the 'span' of the set, where the 'span' is defined as $$S = max(\sum_{j=1}^{N}\sum_{k=1}^{j}q_k) - min(\sum_{j=1}^{N}\sum_{k=1}^{j}q_k) + 1$$To understand problems, a wordy definition is also useful, so here's a story statement:
Timmy the Dog lives on a one-dimensional line. Timmy's home kennel is situated at $x = 0$. Every day, Timmy (being an adventurous pup), either increases his $x$ coordinate by $1$ (with a 50% chance), or decreases his $x$ coordinate by $1$. Each time Timmy visits a new place, he pees on it, marking his territory. After $N$ days, how many places on average will Timmy have visited (including his home kennel)?
An example of $N = 5$, where Timmy the dog starts at $0$, goes to $1$, then $0, -1, -2$ and finally $-1$. The amount of places Timmy has visited in this example is $4$ (${-2,-1,0,1}$).
When I first attempted this problem, I did some pretty silly things, like finding where Timmy ended on average (which didn't really help, because we want to know where Timmy has been). Eventually I sort of willy-wonkered myself back onto track, and now I finally have a solution. Solution is made up of several parts.
Step 1: The Foundation and Realization
The average $S$ (where $S$ is defined to be the span), is defined by the following formula:
$$\bar{S} = \sum_{j = 0}^{\infty}P(j)*j$$
where $P(j)$ is defined as the probability that the random walk has a span of size $j$. At this stage of time, if I can find an expression for $P(j)$, then we can all pack our bags and go home because it would be game over, I could just plug it in (and hopefully simplify it).
From here on, I defined $a$ and $b$ according to the following diagram:
$a$ is defined as $|min(\sum_{j=1}^{N}\sum_{k=1}^{j}q_k)|$ and $b$ is defined as $ max(\sum_{j=1}^{N}\sum_{k=1}^{j}q_k)$ such that $S = a+b+1$.
Now, we can sort of find a formula for $P(j)$:
$$P(j) = \sum_{k = 0}^{j-1}G(N,k,j-k-1)$$
Where $G(n,a,b)$ is the probability that after $n$ days, Timmy has reached $a$ to the left and $b$ to the right (as depicted in the diagram above). We can further crack this formula down with the realization that:
$$G(n,a,b) = Q(n,a,b) - Q(n,a-1,b) - Q(n,a,b-1) + Q(n,a-1,b-1)$$
Where $Q(n,a,b)$ is defined as the probability that Timmy's $x$ coordinate is never less than $-a$, and never greater than $b$. In other words, Timmy is 'confined' for the $n$ days within the parameters $a$ and $b$. So the chance that Timmy actually visits $x = -a$ and $x = b$ is given by $G(n,a,b)$, and for this to be true Timmy needs to be confined by ($a,b$) (in other words $Q(n,a,b)$), but has to exceed both $Q(n,a-1,b)$ and $Q(n,a,b-1)$. (The final terms is added on in a case of inclusion-exclusion, because we over-count).
(Diagram to sort of visualize the inclusion-exclusion)
Putting everything together, we have the following equation:
$$\bar{S} = \sum_{j = 0}^{\infty}j* \sum_{k = 0}^{j-1}(Q(N,k,j - k - 1) - Q(N,k-1,j-k-1) - Q(N,k,j-k-2) + Q(N,k-1,j-k-2))$$
In words, this equation looks at all possible spans that Timmy can attain in $N$ days, then looks at the values of $a,b$ that can be used to get these spans, and sums over everything. However, I found the following rearrangement more useful:
$$\bar{S} = \sum_{a = 0}^{\infty} \sum_{b = 0}^{\infty} (a+b+1)(Q(N,a,b) - Q(N,a-1,b) - Q(N,a,b-1) + Q(N,a-1,b-1)$$
This is instead summing over $a$ and $b$. This can be seen as repeatedly asking "What is the chance that Timmy's minimum $x$ was this value, and maximum $x$ was this value?" Cool.
Step 2: Degeneration over space
I got stuck for a good while. I can remember when I made a further breakthrough. I was walking to McDonald's (I am such a healthy kid) and there's his seat on a hill that's sort of nice. I was lying down on the seat when suddenly I realized "Wait, lots of things cancel out don't they?"
The above is (roughly) what I had sketched in my notepad. Because we are summing over both $a$ and $b$, we can sort of list everything we are summing in a massive table (that extends to infinity). Each cell represents the contribution of each value of $a$ and $b$.
As can be seen, lots of cancelling goes on. For instance, looking at the total number of $Q(N,0,0)$'s, theres $1$ from $a=0,b=0$, there's $-2$ from $a=1,b=0$, there's $-2$ from $a=0,b=-1$, and there's $3$ from $a=1,b=1$, giving a grand total of... $0*Q(N,0,0)$. In fact, a much more startling realization is that whatever values you pick for $a$ and $b$, (for instance $Q(N,x,y)$), you get a total contribution of $((x+y+1)-(x+1+y+1)-(x+y+1+1)+(x+1+y+1+1))*Q(N,x,y)$, or $0*Q(N,x,y)$. Just about now, my internal organs started failing. This was a disaster. I had felt that I was finally getting somewhere, only to find that the answer was... $0$? That's just heartbreaking. Seriously. I remember kneeling on the ground looking at the clouds, thinking "Why me?"
Shortly afterwards, I resumed walking to McDonald's, and I found the flaw in what I had done. It was to do with the fact that I was summing to infinity. I remembered my friends, I and J's voices echoing in my head: "It's bad to play with infinities (something something diverging something something)". For example, the following sum:
$$R = \sum_{j = 1}^{\infty}j - (j+1)$$
Written out, the sum looks something like this:
$$R = (1-2)+(2-3)+(3-4)+(4-5)....$$
If you pick any integer $j$ which is greater than $1$, you will have some term that adds a $j$, and another term that subtracts a $j$, in other words the sum should end up being just $1$. (there are no $2$'s, no $3$'s, no $4$'s, etc.)
BUT, it's clear that something very dodgy is going on. Each term is equal to $-1$, so effectively what we have is
$$R = \sum_{j=1}^{\infty} (-1)$$
which is something super negative (and clearly not equal to $1$). The way I solved this problem with infinities was by bounding my sum. Currently, my sum runs from $a = 0$ to $\infty$, and $b = 0$ to $\infty$. However, for certain values of $a$ and $b$, $G(N,a,b) = 0$. These are sort of like degenerate cells. For instance, if $|a| > N$, (a reminder that $G(N,a,b)$ is the chance that Timmy visits $x = -a$ as his minimum and $x = b$ as his maximum), then $G(N,a,b) = 0$, because Timmy simply can't reach $a$ in $N$ days. Similarly, if $b > N$, $G(N,a,b) = 0$. In fact, if we draw a table like we drew last time:
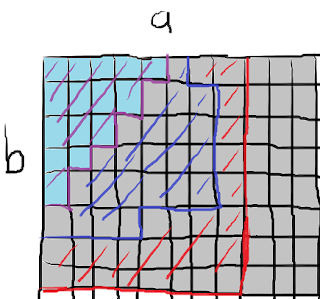
For the case of $N = 4$, the above image represents which values of $a$ and $b$ give positive $G(N,a,b)$. The light blue squares mean that they are "meaningful", and the grey squares mean that they are 'degenerate matter' (I feel so cool right now, but I'm pretty sure in like a year I'll read this and think "lol thats such a dumb name"), in other words they have no bearing on the actual sum.
So, we have to bound our sum, to something finite. The REALLY COOL THING is, that we can bound our sum however we like, as long as we bound it like within the degenerate matter. (this probably won't even make sense to me later, I'll just draw a diagram):
For instance, I could sum up all the cells within the purple boundary. This might seem like the most sensible sum, as I'm not taking any degenerate matter into account. But, I also have the option of the blue and red boundaries, because the degenerate matter doesn't actually change the sum (because each of the grey squares have a value of $0$), but can still make the sum simpler. I used my animal instincts, and picked to sum within the red boundary.
In other words, I was limiting $a$ and $b$ to some finite value. For some reasons (that are really half-baked, so just roll with it), I wanted to make the limit of $a$ and $b$ really big. So, after taking all that into account, we have (drumroll):
$$\bar{S} = \sum_{a = 0}^{C} \sum_{b = 0}^{C} (a+b+1)(Q(N,a,b) - Q(N,a-1,b) - Q(N,a,b-1) + Q(N,a-1,b-1)$$
where $C >> N$. $C$ is just really big. Just roll with it. Now remember how lots of things cancelled? The same thing happens here. If the cell $(x,y)$ is included, then it is completely cancelled if the cells $(x+1,y)$, $(x,y+1)$, and $(x+1,y+1)$ are included. Because we picked the red boundary, suddenly our expression becomes:
$$E = 3 + 2N - 2\sum_{j=0}^{N}Q(N,j,C)$$
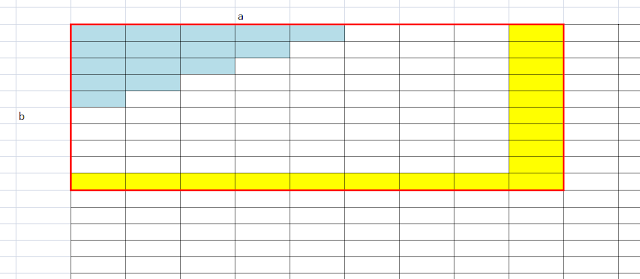
To explain this, feast your eyes upon this excel table (because I'm too lazy to draw anymore):
$$E = 3 + 2N - 2\sum_{j=0}^{N}Q(N,j,C)$$
To explain this, feast your eyes upon this excel table (because I'm too lazy to draw anymore):
This is another example of $N = 4$. The light blue squares represent the positive valued squares. However, we know that almost all the squares completely cancel. The only values of $(a,b)$ that don't completely cancel are highlighted in yellow. Furthermore, realizing that $Q(N,c,d) = 1$ where either $c > N$ or $d > N$ (because $Q(N,x,y)$ is the chance that Timmy is bounded within $a=x$ and $b=y$, and the chance that he's bounded within $(N,N)$ or anything greater is $1$.) simplifies things. Considering just the right column of yellow squares, the top portion is $-\sum_{j=0}^{N}Q(N,C,j)$. (bloody hell I thought writing the proof was going to be easy but there's so many things I have to write, I should really learn how to write with proper math symbols and not words lol). In short, the reason is because each a yellow square at $(C,k)$ provides a $(C+k+1)*Q(N,C,k)$, but the yellow square directly underneath it provides a $-(C+k+2)*Q(N,C,k)$, in other words a net of $-Q(N,C,k)$. The bottom portion of the column is just a series of $-1$'s in a row (for much the same reasoning). The row of yellow cells on the bottom is the exact same as the column of yellow cells on the right (due to the symmetry of $a$ and $b$). The bottom right cell's positive contribution sort of 'rectifies' all the negatives.
(This is probably not going to make much sense to anyone is it lol)
Step 3: Cracking of the nuts
So what we want to find now is $Q(N,j,C)$ for $j \geq 0$. We are slowly getting somewhere. By messing around, I found another 'cracking' method (a way to decompose what we want into different things).
$Q(n,a,b)$ is equal to $0.5*Q(n-1,a+1,b) + 0.5*Q(n-1,a-1,b)$, because out of the $n$ moves that Timmy makes, the first move is either right or left. If it's right, the chance that overall Timmy is constrained within $(a,b)$ is going to be the half times the chance that within $n-1$ days that he is constrained within $(a+1,b-1)$. The same applies if Timmy moves left on the first day. These two outcomes are shown by the purple/red lines.
After decomposing the whole lot bit by bit, what we end up with is
$$E = 2 + \sum_{j=1}^{N-1}Q(j,0,C)$$
(Here we use the fact that because $C >> N$, then $C - 1 = C$ pretty much. In essence, we can choose $C$ however big we like, so it won't have any bearing on our sum.)
Step 4: Analyzing the Truncated Pascal
Lets take a moment to think of the significance of $Q(j,0,C)$. Pretty much, this expression is the probability that in $j$ days, Timmy never goes to the left of his kennel (because $a$ is $0$). We can represent this information in a 'truncated Pascal Triangle':
The 'truncated Pascal triangle' is a representation of the paths that Timmy can take, if he is never to go left of his kennel. (hence $x \geq 0$). $j$ in the table represents the number of moves that Timmy makes. Pretty much it's truncated, except it works just as a normal Pascal triangle works. The numbers represent how many ways there are of Timmy arriving at that particular $x$ coordinate after $j$ days. What's interesting to us however is the probability that after $j$ days Timmy has not moved left of his kennel, i.e. we are interested (indirectly?) in the sum of each row (shown on the right).
Looking at those numbers invokes a sense of awe within me. Because these are all numbers found on the PASCAL'S TRIANGLE!!! (the normal one). To be precise, the sum for $j = n$ will be $n \choose {\lfloor \frac{n}{2} \rfloor}$. This is all well and good, but finding a reason for this match up is actually quite hard. In fact, I pretty much couldn't find no reason for it. It's almost like I found a KFC box on the ground, except it was filled with rocks. My heart was crushed.
So here I was, racking my brains for some way to determine the sum for any value of $j$. (I actually came up with this method a long time ago, but it was a completely idiotic method so I was like "haha nah"). Basically, from $j = 0$ to $j = 1$, there's only one path (so the sum doesn't change). From $j = 1$ to $j = 2$, the path splits into two, so the new sum is twice the old sum. From $j = 2$ to $j = 3$, one of the paths only has one route to take, and one of the paths has two routes to take. If I was incredibly naive, I'd say that $S_{new} = \frac{2+1}{2} S_{old}$ where $S_{new}$ is the new sum and $S_{old}$ is the old sum. For $j = 2$ to $j = 3$, this actually works. Then for $j = 3$ to $j = 4$, again, all the paths split into two, so its no surprise that the new sum is twice the old sum. For $j = 4$ to $j = 5$, one of the endpoints only has one choice (so as not to go to $x = -1$), but all the other endpoints have two choices respectively. Using my incredibly naive method, we would expect $S_{new} = \frac{2+2+1}{2}S_{old}$. AND IT WORKS. In fact, this incredibly naive definition works for all values of $j$ I tested.
Now, this is incredibly strange. The transitions from $j = odd$ to $j = even$, where the new sum is twice the old, is nothing strange. That's expected. But the method I was using for the transitions from $j = even$ to $j = odd$ was just completely nuts. The only way it would work is if (for some reason) the first term in each row where $j = even$ is the average of the values of the entire row. It's clear from the diagram that this is the case for the values of $j$ shown. (for instance, for $j = 6$, the average of the row is $\frac{SUM}{4} = 5$, and the first value is $5$). So, if I could prove that the first value of each row for $j = even$ is the average of the values of the entire row, I could use my method to find the Sums, then find the probabilities, then I could find the span and I would be a very happy man.
I thought I'd try my hand at induction (simple induction, where we assume true for $j = k$ and prove true for $j = k+2$). Firstly, some notation. $p_{f,g}$ is the $g$th number on the $j = f$ row. From the table given, it is evident that the statement is true for $j = 2$. Assuming true for $j = k$, we have that:
$$p_{j,1} = \frac{p_{j,2}+p_{j,3}+...p_{j,0.5j+1}}{0.5*j}$$
Now we wish to prove statement for $j = k+2$ (because we are only interested in $j = even$)
$$RTP: p_{j+2,1}= \frac{p_{j+2,2}+p_{j+2,3}+...p_{j+2,0.5j+2}}{0.5*j+1}$$
Now, from the pascal's triangle, we can observe that:
$$p_{j+2,1} = p_{j,1} + p_{j,2}$$
and for $k > 1$:
$$p_{j+2,k} = p_{j,k-1} + 2p_{j,k} + p_{j,k+1}$$
Using these relationships, (and using our assumption) we finally arrive at:
$$RTP: p_{j,1} = \frac{j+4}{3j}p_{j,2}$$
So now, we are nearing the end. All we have to is prove this final statement, and we have all the pieces ready. It's been a long road, but we are nearly there.
Step 5: The Final Destination
So at this point of time, what we want is a method to relate $p_{j,1}$ to $p_{j,2}$. Luckily, there's a method that does exactly that. $p_{j,1}$ can be understood as the number of unique paths that Timmy could take from one corner of a square to the opposite corner without crossing the diagonal joining the corners, as shown here:
The purple line represents what Timmy must not cross, and the red is an example path for Timmy.
Evidently, the total number of paths that Timmy can take to get to the other corner is $j \choose \frac{j}{2}$. What we want to do is separate the paths that strictly stay above the purple path from those that pass below the purple path. The tactic we use is this. Suppose we have a path that drops below the purple line. That means at some point, it will venture to the right of the purple line. Now, reflect all the moves one move after Timmy has crossed the purple line.
For instance, this red path crosses the purple line along it's journey. We let Timmy take one step into the beyond, and then reflect all his subsequent moves, so that if he were to move right make him move up instead, and if he were to move up then move right instead. We can easily see that all such paths will end up at a point one below and one to the right of the intended corner. From the facts: (1) All paths that cross the purple line can be flipped to produce a path that ends at this new point (2) All paths that go to the new point can be generated by flipping a path that crosses the purple line (3) All paths that cross the purple line, when inverted, produce a unique path, we can conclude that the number of paths that cross the purple line is equal to the number of paths that reach the alternate end point, namely $j \choose {\frac{j}{2}-1}$
Using this logic, we can get an expression for $p_{j,1}$:
$$p_{j,1} = j \choose \frac{j}{2} - j \choose {\frac{j}{2}-1}$$
We can use very similar logic to get an expression for $p_{j,2}$:
$$p_{j,2} = j \choose {\frac{j}{2}-1} - j \choose {\frac{j}{2}-2}$$
Combining these two formulas, we can find the relationship between $p_{j,1}$ and $p_{j,2}$, and lo and behold:
$$p_{j,1} = \frac{j+4}{3j}p_{j,2}$$
Bam. We find exactly what we need to prove the induction, that the beginning of each important row of the truncated pascal is the average of the entire row. From here on, life is a breeze. We just throw everything together to get a formula. There are heaps of ways to express the formula. The most comprehensive is:
$$\bar{S} = 2 + \sum_{j = 1}^{N-1} j \choose {\lfloor \frac{j}{2} \rfloor} * \frac{1}{2^j}$$
but the one I like the most is:
$$\bar{S} = 2 + 2(\frac{1}{2} + \frac{1*3}{2*4} + \frac{1*3*5}{2*4*6} + ... + \frac{1*3*5*...*(N-2)}{2*4*6*...*(N-1)})$$
for odd values of $N$.
I was going to read over what I had written, but I'm burnt out.
The prediction is in green, a test is in blue. As can be seen, it pretty much fits exactly. This is a plot of $\bar{S}$ against $N$
It shouldn't converge, but I'll leave the proving of that to another day.